Industrijska elektronika

Industrijska elektronika	Autor: Dragan Marinković

PROJEKTOVANJE VLASTITOG SCADA SISTEMA, II DEO

Da je Ahil znao gde će biti pogođen sigurno bi naručio pancir ili što je sigurno, zažalio što se nije sav okupao. Da, jedno je sigurno, današnji inženjeri i projektanti programske i elektronske podrške informaciono - upravljačkog sistema ne smeju imati Ahilovu petu jer tada neće umreti samo Ahil.

U prošlom broju časopisa je rečeno da se kombinovanjem unutarnjih stanja računara, njegovih ulaza i izlaza može dobiti funkcija odziva kakva se traži za određenu procesnu primenu. Međutim jedno je traženje, tj modelovanje i iznalaženje funkcije prenosa za proces - objekt upravljanja a drugo je traženje funkcije prenosa za upravljač, u ovom slučaju računar. Koji su razlozi ovakvog tretiranja problematike. Razlog je motivisan željom da čitaoc stekne osećaj da je sve što se povezuje sa računarom jeste ili postaje diskretne prirode. Dakle počevši od vremenski kontinualnih sistema, kontinualnih matematičkih opisa krećemo se prema linea-rnim diskretnim (i u krajnjoj liniji digitalnim) sistemima upravljanja. Pa krenimo.

Kontinulalni sistemi bez i sa povratnom spregom

U suštini radilo se o sistemu (procesu) sa jednim ulazom i jednim izlazom ili o multivarijabilnom sistemu (sa više promenljivih na ulazu i više promenljivih na izlazu) uvek se može opisati prenosnom funkcijom (samo linearni sistemi) G(s) i prenosnom matricom G(s) respektivno (odnosno matricom sistema A, fundamentalnom matricom (s), ako je sistem opisan jednačinama u prostoru stanja). Imenilac u prenosnoj funkciji naziva se karakteristična je-dnačina sistema. A poznato je da slobodan (svojstveni) odziv sistema (stabilnost sistema) zavisi od korena karakteristične jednačine sistema. Iz matrice sistema A dobijamo svojstveni polinom (det(sI-A)) čiji koreni(sopstvene vrednosti) daju odgovor o stabilnosti sistema (promenljive stanja i promenljive izlaza asimptotski treba da teže nuli u vremenskom domenu) dok sama za sebe fundamentalna matrica predstavlja slobodno rešenje sistema i osnov za određivanje odziva za primenjeno upravljanje u(t). Isto važi kad se sistem poveže tako da ima povratnu spregu, naime i tada karakteristična jednačina opisuje ponašanje sistema (sistem opisan preno-snom funkcijom) a matrica A i matrica prelaza (s) se zamenjuju matricom zatvorenog sistema, Az i z(s) respektivno (sistem opisan u prostoru stanja).

3b41.gif (6715 bytes)
Slika 1. Principijelni blok dijagram klasičnog jednokoturnog sistema automatskog upravljanja sa jediničnom povratnom spregom

Ako predstavimo sistem prenosnom funkcijom (ili prenosnom matricom) onda nemamo nikakvu info-rmaciju o unutrašnjoj strukturi sistema već se samo uspostavlja odnos između ulaza i izlaza. Međutim ako u opisivanju sistema pođemo od promenljivih stanja tada imamo minimalnu količinu informacija o sistemu, koje zajedno s poznatom funkcijom na ulaz u sistem, u(t), jednoznačno određuje odziv ili dalje ponašanje sistema. Osim toga ako sistem opisujemo preko promenljivih stanja tada sistem opisujemo skupom diferencijalnih jednačina prvog reda umesto jedne jedine jednačine višeg reda. Ovim je problem uprošćen tako da se može koristiti računar još efika-snije, naročito ako je sistem sa više ulaza i izlaza.

Upotreba računara se u ovoj da tako kažem prvoj fazi svodi na predstavljanje i ispitivanje (analiza) osobina sistema upravljanja. U drugoj fazi, dakle posle utvrđivanja osobina upravljanja, računarom (mikroračunarom) modeliramo funkciju odziva (sinteza) odnosno dejstava na sistem (objekt upravljanja), no o tome u pregledu diskretnih sistema.
Vektorsko - matrični oblik dinamičkih jednačina sistema (u prostoru stanja) koji jednoznačno određuju odnos između izlaza, ulaza i stanja sistema je (jedna funkcija na ulazu i na izlazu sistema) :

dX/dt = A X(t) + b u(t)
Y(t) = cT X(t) + d u(t)

gde su;
A - matrica sistema (objekta upravljanja)
X- vektor promenljivih stanja
b - vektor upravljanja
u(t) - funkcija upravljanja
Y(t) - skalarni izlaz (izlazna veličina, upravljana veličina)
cT - vektor izlaza

A za multivarijabilni sistem dinamičke jednačine sistema glase:

dX/dt = A X(t) + B U(t)
Y(t) = C X(t) + D U(t)

gde su:
B - matrica upravljanja
U(t) - vektor ulaza (f-ja upravlj.)
Y(t) - vektor izlaza
C - matrica izlaza

Treba reći da se opisivanje sistema odnosi na slučaj linearnog kontinualnog sistema s parametrima invarijantnim u vremenu. Dakle vidi se da izlazi iz linearnog sistema mogu da zavise i od ulaznih signala. Matrice A i X(t) ostaju nepromenjene u pogledu dimenzija u oba slučaja.
U slučaju klasičnog jednokonturnog sistema automatskog upravljanja s jediničnom povra-tnom spegom ( sl. 1 ) upravljački signal U(t) se formira dejstvom greške e(t)=Xw-X ( tj r(t)-y(t)) između vodeće veličine Xw ( r(t)) i regulirane veličine X (zapravo izlazne veličine Y(t) po drugoj terminologiji) na odgovarajući regulator ili korekcioni element. Pogledajmo kako dejstuje npr PID regulator (sl.3). Pojednostavljena prenosna karakteristika PID dejstva glasi :

YPID = K ( Xd + 1/Tn . Xd . t + Tv . (dxd/dt))

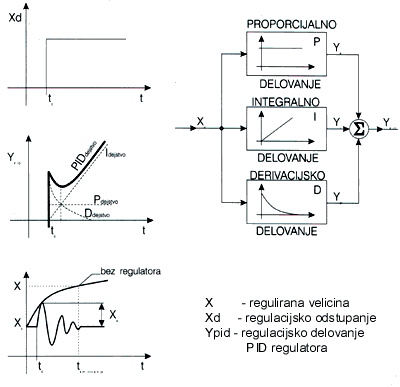
Vidi se da D delovanje prvo počinje delovanje, i može se prikazati kao P delovanje s vrlo velikim pojačanjem. Drugo je delovanje proporcionalno, koje je prema D delovanju malo, ali koje takođe nastupa u prvom trenutku. Treće delovanje je I delovanje koje dolazi najkasnije ali koje s vremenom raste, pa regulacijsko odstupanje smanjuje prektično na nulu. PID regulator sjedinjuje sve dobre osobine osnovnih vrsta re-gulatora. 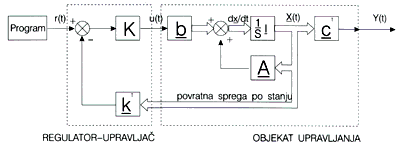Pomoću D delovanja deluje veoma brzo i unapred sprečava velika regulacijska odstupanja, P delovanje mu daje stalno i dovoljno jako pojačanje, a i delovanje mu osigurava tačno i potpuno otklanjanje regulacijskog odstupanja Xd .Međutim pri opisivanju objekta upravljanja pomoću promenljivih stanja, klasična koncepcija povratne sprege se proširuje tako da se umesto povratne sprege izlaza, kao povratne sprege koriste svih n promenljivih stanja (sl. 2).

3b42.gif (19405 bytes)
Slika 2. Blok dijagram upravljanja pomoću linearnih povratnih sprega promenjivih stanja

Jednačina stanja i jednačina izlaza sistema sa povratnom spregom u tom (jedna funkcija na ulazu i na izlazu sistema) slučaju glasi:

dX/dt = A Z X(t) + K b r(t),
A Z= A - K b kT
Y(t)=cT X(t)
U(t)=K ( r(t) - ( k1 X1(t) + k2 X2(t) + ... + kn Xn(t)))

Upravljački signal se formira, kao što se vidi, na bazi promenljivih stanja i vodeće ulazne veličine r(t) (promenljive vođenja-referentne ulazne veličine)).
Bitno je ovde napomenuti da izbor promenljivih stanja (prostor stanja) nije jednoznačno određen, jer se dinamika sistema može opisati izborom različitih promenljivih pa u pogledu broja mogućnosti izbora promenljivih stanja sistem nema ograničenja. U slučaju mehaničkih, električnih i nekih hemijskih sistema izbor promenljivih stanja je nešto olakšan time što se za promenljive mogu birati promenljive pomoću kojih se izražavaju međusobno nezavisne količine energije akumulirane u sistemu. Tako npr. promenljive stanja mogu biti brzina, položaj, temperatura, pritisak, struja, napon itd.

3b43.gif (52998 bytes)
Slika 3.Princip delovanja kontinualnog PID regulatora (upravljača)
PID dejstvo brzo otklanja poremećaj i vraća regularnu veličinu na željenu prvobitnu vrednost Xo. Pogodno je za objekte upravljanja koji sadrže više kapacitvnih elemenata.

Pročitajte više o ovoj temi

WEB link

	LOOKOUT^®
	Osnove prikupljanja podataka i upravljanja WASCAD sistemi
	Projektovanje vlastitog SCADA sistema I deo
	Lookout

	Razvojni sistemi
	Knjige
	CD izdanja
Posetite stranu Teme po oblastima i informišite se o člancima iz sličnih oblasti!